פיגור 1 ווייזט א געוויינטלעכע געשלאצטע כוואַליע-פירער דיאַגראַמע, וואָס האט אַ לאַנגע און שמאָלע כוואַליע-פירער סטרוקטור מיט אַ שפּאַלט אין דער מיט. די שפּאַלט קען ווערן גענוצט צו טראַנסמיטירן עלעקטראָמאַגנעטישע כוואַליעס.

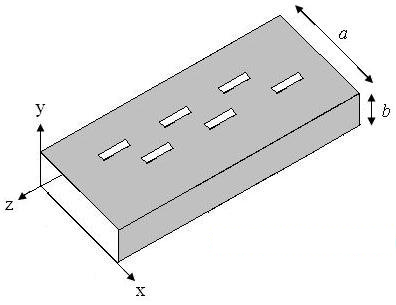
פיגור 1. געאמעטריע פון די מערסטע פארשפרייטע סלאטיד וועיווגייד אנטענעס.

די פראָנט-ענד (Y = 0 אָפענע פּנים אין דער xz פלאַך) אַנטענע ווערט געשפּיצט. דער ווייטער עק איז געוויינטלעך אַ קורץ קרייַז (מעטאַלישע אָפּצוימונג). דער כוואַליע-פירער קען ווערן אויפֿגעוועקט דורך אַ קורץ דיפּאָל (געזען אויף דער צוריק פון דער קאַוויטי שפּאַלט אַנטענע) אויף דער בלאַט, אָדער דורך אַן אַנדער כוואַליע-פירער.

צו אָנהייבן אַנאַליזירן די פיגור 1 אַנטענע, לאָמיר קוקן אויף דעם קרייַז מאָדעל. די כוואַליע פירער אַליין אַקט ווי אַ טראַנסמיסיע ליניע, און די סלאָץ אין די כוואַליע פירער קענען זיין געזען ווי פּאַראַלעל (פּאַראַלעל) אַדמיטאַנסאַז. די כוואַליע פירער איז קורץ-געשלאסן, אַזוי די אַפּראָקסימאַטיווע קרייַז מאָדעל איז געוויזן אין פיגור 1:

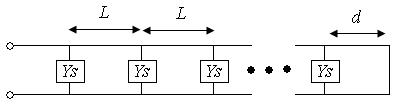
פיגור 2. קרייַז מאָדעל פון סלאַטיד כוואַליעגייד אַנטענע.

דער לעצטער שפּאַלט איז אַ דיסטאַנץ "d" צום סוף (וואָס איז קורץ-געשלאָסן, ווי געוויזן אין פיגור 2), און די שפּאַלט עלעמענטן זענען צעשפּרייט אַ דיסטאַנץ "L" פון יעדן אַנדערן.

די גרייס פון דער רינע וועט געבן א גייד צו דער כוואַליע לענג. די גייד כוואַליע לענג איז די כוואַליע לענג אינעם כוואַליע גייד. די גייד כוואַליע לענג ( ) איז אַ פונקציע פון דער ברייט פון דער כוואַליע גייד ("a") און דער פרייער פּלאַץ כוואַליע לענג. פֿאַר דעם דאָמינאַנטן TE01 מאָדע, די גיידאַנס כוואַליע לענג זענען:

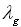
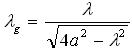
די דיסטאַנץ צווישן דעם לעצטן שפּאַלט און דעם סוף "d" ווערט אָפט אויסגעקליבן צו זיין אַ קוואַרטער כוואַליע-לענג. דער טעאָרעטישער צושטאַנד פון דער טראַנסמיסיע ליניע, די קוואַרטער-כוואַליע-לענג קורץ-קרייז ימפּידאַנס ליניע טראַנסמיטטעד אַראָפּ איז אָפֿן קרייז. דעריבער, פיגור 2 רעדוצירט צו:

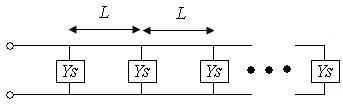
בילד 3. געשלאטעטע כוואַליעגייד קרייַז מאָדעל ניצנדיק קוואַרטער-כוואַליע לענג טראַנספאָרמאַציע.

אויב פּאַראַמעטער "L" ווערט אויסגעקליבן צו זיין אַ האַלבע כוואַליע-לענג, דאַן ווערט די אַרייַנגאַנג ž אָהמישע אימפּעדאַנס געזען ביי אַ האַלבע כוואַליע-לענג דיסטאַנץ z אָהמס. די "L" איז אַ סיבה פאַר דעם פּלאַן צו זיין אַרום אַ האַלבע כוואַליע-לענג. אויב די כוואַליע-פירער שפּאַלט אַנטענע איז דיזיינד אויף דעם וועג, דאַן קענען אַלע שפּאַלטן ווערן באַטראַכט פּאַראַלעל. דעריבער, קען די אַרייַנגאַנג אַדמיטאַנס און אַרייַנגאַנג אימפּעדאַנס פון אַ "N" עלעמענט שפּאַלט אַרעי שנעל ווערן קאַלקולירט ווי:

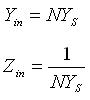
די אינפוט אימפעדאַנס פון די כוואַליעגייד איז אַ פונקציע פון די שפּאַלט אימפעדאַנס.

ביטע באַמערקן אַז די אויבן דערמאָנטע פּלאַן פּאַראַמעטערס זענען בלויז גילטיק ביי איין פרעקווענץ. ווי די פרעקווענץ גייט ווייטער פון דאָרט ווי דער וועיווגייד פּלאַן אַרבעט, וועט זיין אַ דעגראַדאַציע אין דער פאָרשטעלונג פון דער אַנטענע. ווי אַ בייַשפּיל פון טראַכטן וועגן די פרעקווענץ קעראַקטעריסטיקס פון אַ סלאַטיד וועיווגייד, וועט מען ווייַזן מעסטונגען פון אַ מוסטער ווי אַ פונקציע פון פרעקווענץ אין S11. דער וועיווגייד איז דיזיינד צו אַרבעטן ביי 10 GHz. דאָס ווערט געפֿיטערט צו דער קאָאַקסיאַלער פֿיטער ביי דער אונטערשטער טייל, ווי געוויזן אין בילד 4.

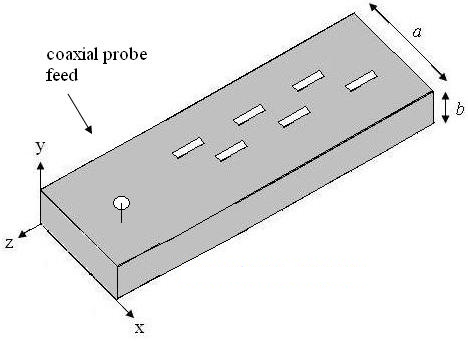
פיגור 4. די געשלאצטע כוואַליעפירער אַנטענע ווערט געפיטערט דורך אַ קאָאַקסיאַל פידער.

דער רעזולטאַט S-פּאַראַמעטער פּלאַנעווען ווערט געוויזן אונטן.

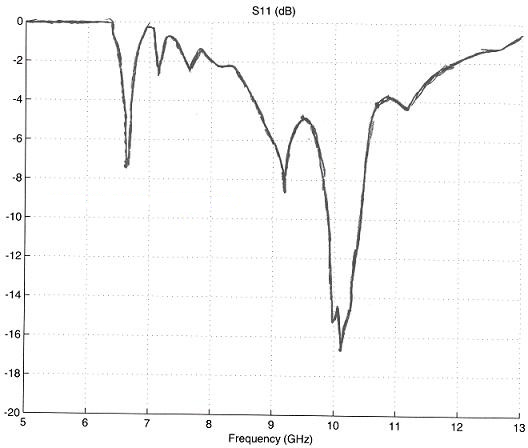
באַמערקונג: די אַנטענע האט אַ זייער גרויסן דראָפּ-אָף אויף די S11 ביי בערך 10 GHz. דאָס ווייזט אַז רובֿ פון די מאַכט קאַנסאַמשאַן ווערט שטראַלן ביי דעם אָפטקייט. די אַנטענע באַנדברייט (אויב דעפינירט ווי S11 איז ווייניקער ווי -6 dB) גייט פון בערך 9.7 GHz צו 10.5 GHz, געבן אַ פראַקשאַנאַל באַנדברייט פון 8%. באַמערקט אַז עס איז אויך אַ רעזאָנאַנס אַרום 6.7 און 9.2 GHz. אונטער 6.5 GHz, אונטער די קאַטאָף כוואַליעגייד אָפטקייט און כּמעט קיין ענערגיע ווערט נישט שטראַלן. די S-פּאַראַמעטער פּלאַנעווען געוויזן אויבן גיט אַ גוטע געדאַנק פון וואָס באַנדברייט סלאַטיד כוואַליעגייד אָפטקייט קעראַקטעריסטיקס זענען ענלעך צו.

דער דריי-דימענסיאָנאַלער שטראַלונג מוסטער פון אַ געשלאָטענעם כוואַליעפירער ווערט געוויזן אונטן (דאָס איז קאַלקולירט געוואָרן מיט אַ נומערישן עלעקטראָמאַגנעטישן פּעקל גערופן FEKO). דער געווינס פון דער אַנטענע איז אַרום 17 dB.

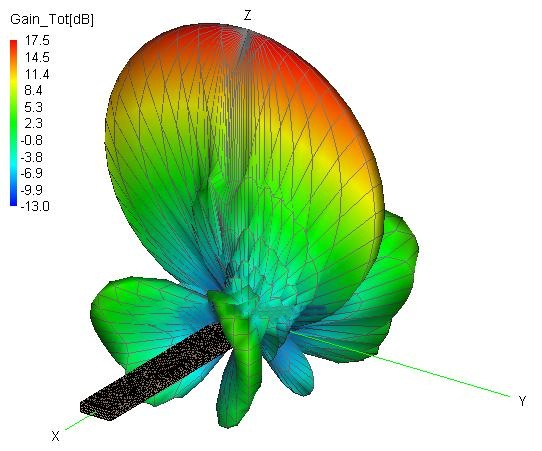
באַמערקט אַז אין דער XZ פלאַך (H-פּלאַן), איז די שטראַל ברייט זייער שמאָל (2-5 גראַד). אין דער YZ פלאַך (אָדער E-פּלאַן), איז די שטראַל ברייט פיל גרעסער.